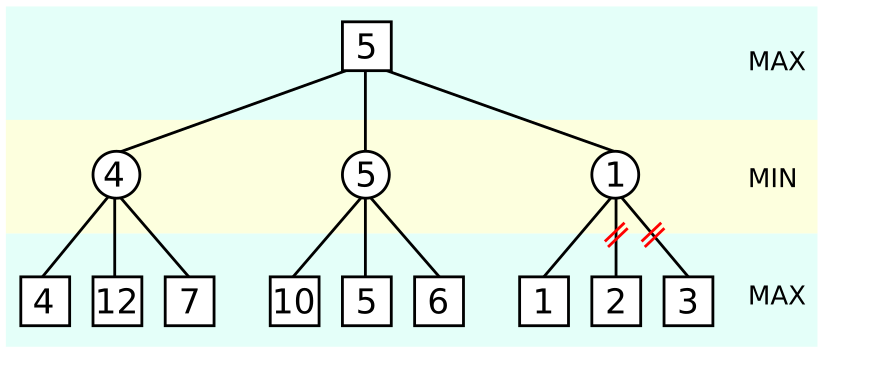
La poda alfa beta es una técnica de búsqueda que reduce el número de nodos evaluados en un árbol de juego por el algoritmo Minimax. Se trata de una técnica muy utilizada en programas de juegos entre adversarios como el ajedrez, el tres en raya o el Go.
Entre los pioneros en el uso de esta técnica encontramos a Arthur Samuel, D.J Edwards y T.P. Hart, Alan Kotok, Alexander Brudno, Donald Knuth y Ronald W. Moore.
El problema de la búsqueda Minimax es que el número de estados a explorar es exponencial al número de movimientos. Partiendo de este hecho, la técnica de poda alfa-beta trata de eliminar partes grandes del árbol, aplicándolo a un árbol Minimax estándar, de forma que se devuelva el mismo movimiento que devolvería este, gracias a que la poda de dichas ramas no influye en la decisión final.
Desarrollo del Algoritmo:
La búsqueda minimax es primero en profundidad, por ello en cualquier momento sólo se deben considerar los nodos a lo largo de un camino en el árbol.
La poda alfa-beta toma dicho nombre de la utilización de dos parámetros que describen los límites sobre los valores hacia atrás que aparecen a lo largo de cada camino.
- α es el valor de la mejor opción hasta el momento a lo largo del camino para MAX, esto implicará por lo tanto la elección del valor más alto
- β es el valor de la mejor opción hasta el momento a lo largo del camino para MIN, esto implicará por lo tanto la elección del valor más bajo.
Esta búsqueda alfa-beta va actualizando el valor de los parámetros según se recorre el árbol. El método realizará la poda de las ramas restantes cuando el valor actual que se está examinando sea peor que el valor actual de α o β para MAX o MIN, respectivamente.
El desarrollo del algoritmo en pseudocódigo será el siguiente:
función alfabeta(nodo //en nuestro caso el tablero, profundidad, α, β, jugador)
si nodo es un nodo terminal o profundidad = 8
devolver el valor heurístico del nodo
si jugador
para cada hijo de nodo
α := max(α, alfabeta(hijo, profundidad+1, α, β, jugador))
si β≤α
break (* poda β *)
devolver α
si no
para cada hijo de nodo
β := min(β, alfabeta(hijo, profundidad+1, α, β, jugador))
si β≤α
break (* poda α *)
devolver β
(* Llamada inicial *)
alfabeta(origen, profundidad, -infinito, +infinito, jugador_deseado)
Ejemplo del Algoritmo:

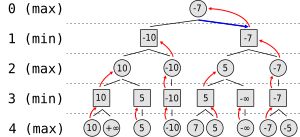
La figura muestra un ejemplo de la poda alfa-beta. Cada nivel representa la jugada de los jugadores MAX y MIN, que tendrán que definir un valor α o β respectivamente.
A continuación se presenta un ejemplo de aplicación del algoritmo para el árbol de la figura. En ella los nodos podados al aplicar el algoritmo se presentan sombreados en gris.
Comenzamos con la búsqueda de primero en profundidad. El padre de los nodos hoja más a la izquierda, etiquetados con 5 y 6 respectivamente, deberá escoger un valor β al tratarse de un nivel MIN, esto implica que deberá escoger el valor mínimo entre dichos nodos, es decir 5.
Siguiendo el desarrollo, se expandirán el resto de sucesores del padre. En este caso se expande el camino que conduce a los nodos hoja 7 y, buscando un valor β menor, el nodo etiquetado con 4. En este momento el valor momentáneo de β en ese nivel es 4 (el mínimo entre 7 y 4). Esto implica que en este momento en el nivel superior, el padre del nodo que etiquetamos anteriormente con β igual a 5, y de este β igual a 4 momentáneo, debe decidir el mejor valor, el más alto al encontrarse en un nivel MAX), si siguiéramos expandiendo hijos del nodo MIN padre de 7 y 4, sólo podríamos conseguir valores menores a 4, lo que seguiría implicando una elección de la jugada izquierda en el nivel MAX, por lo tanto, podemos podar el resto de hijos, tal y como se muestra en la figura.
El resto del desarrollo del árbol se seguiría utilizando los criterios mencionados con anterioridad.







.jpg/220px-HD.3F.191_(11239892036).jpg)